Star-shaped Parameterization
Interpolation over equally spaced angles
| Polygonal Outline | Smooth Outline |
|---|---|
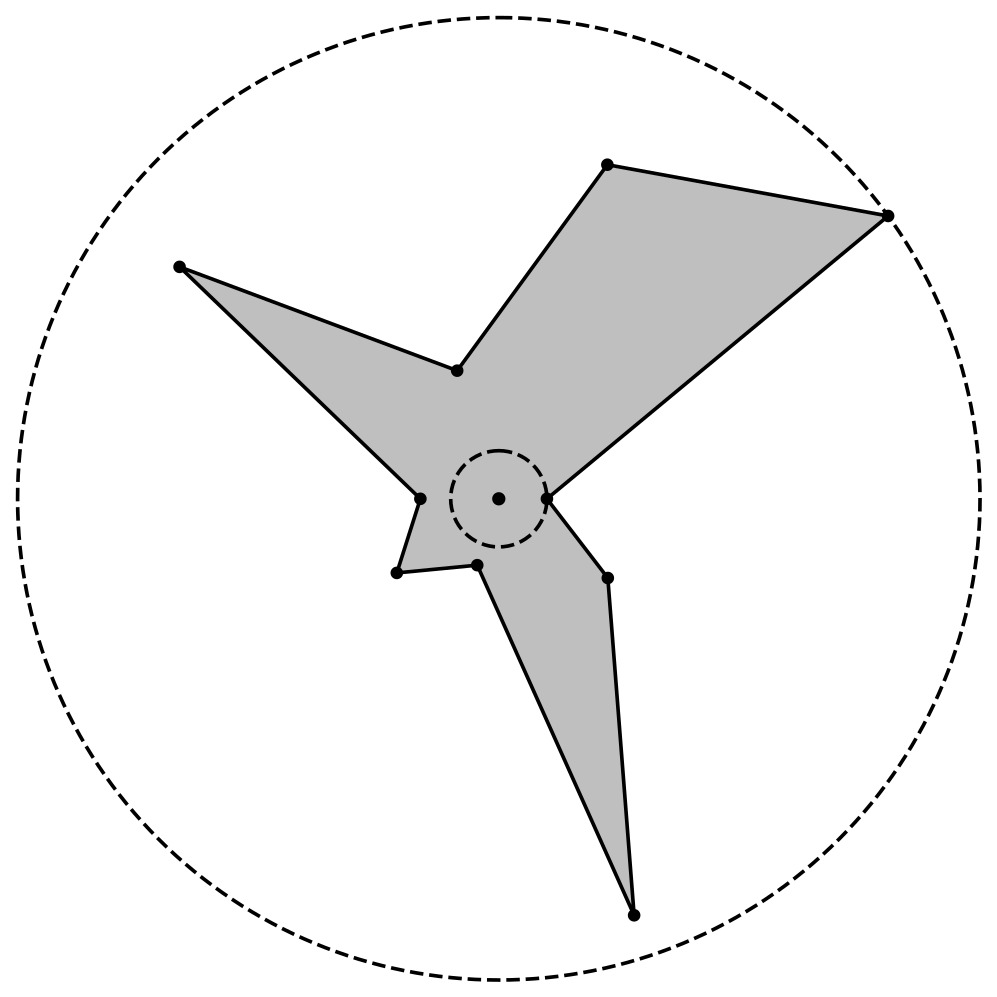 |
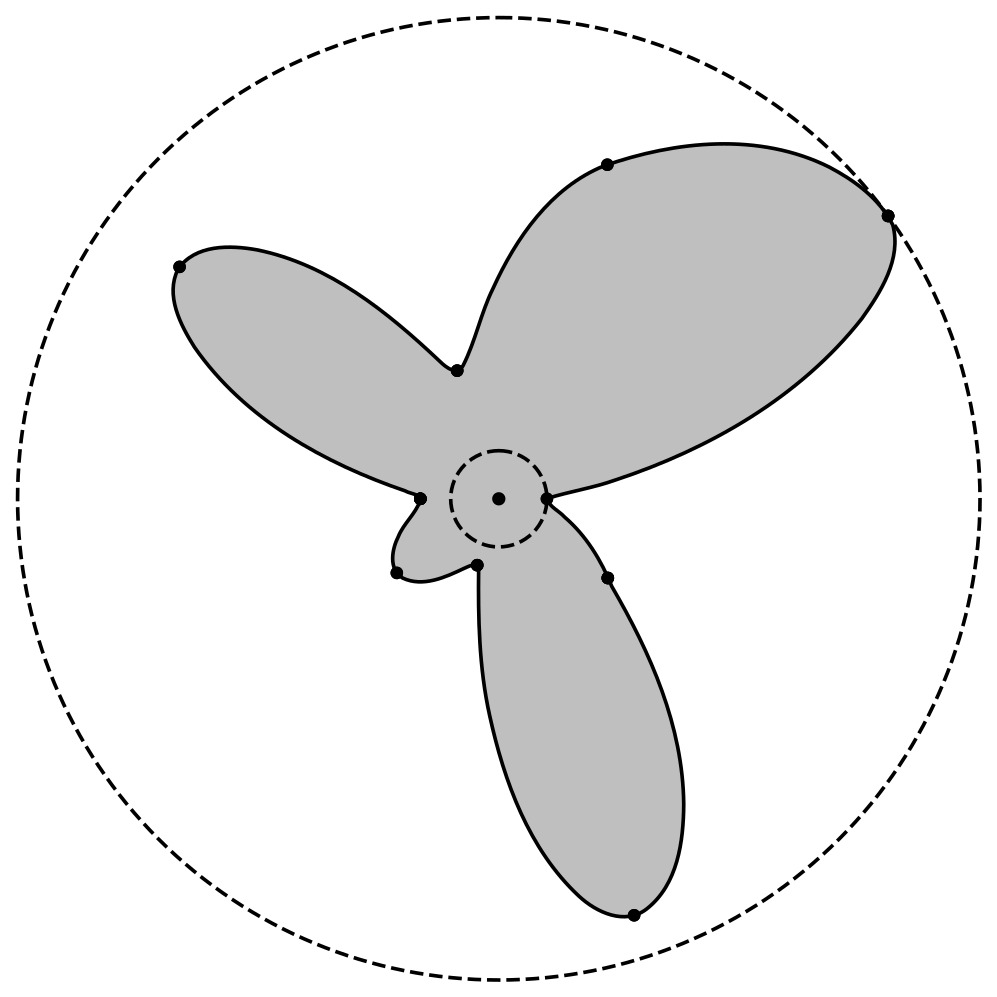 |
Distance vs. Growth Process
| Distance based | Growth Process |
|---|---|
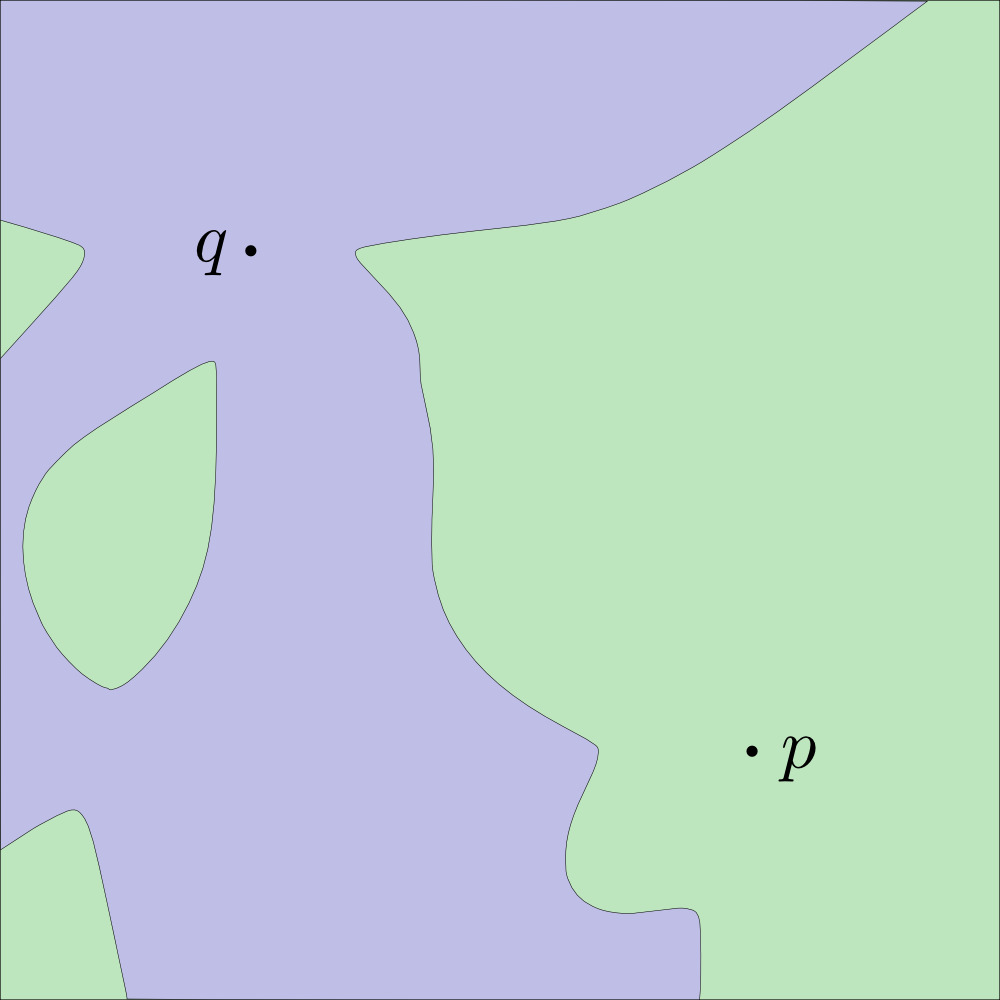 |
 |
Distance vs. Growth Process
| Distance based | Growth Process |
|---|---|
 |
 |
Distance vs. Growth Process
| Distance based | Growth Process |
|---|---|
 |
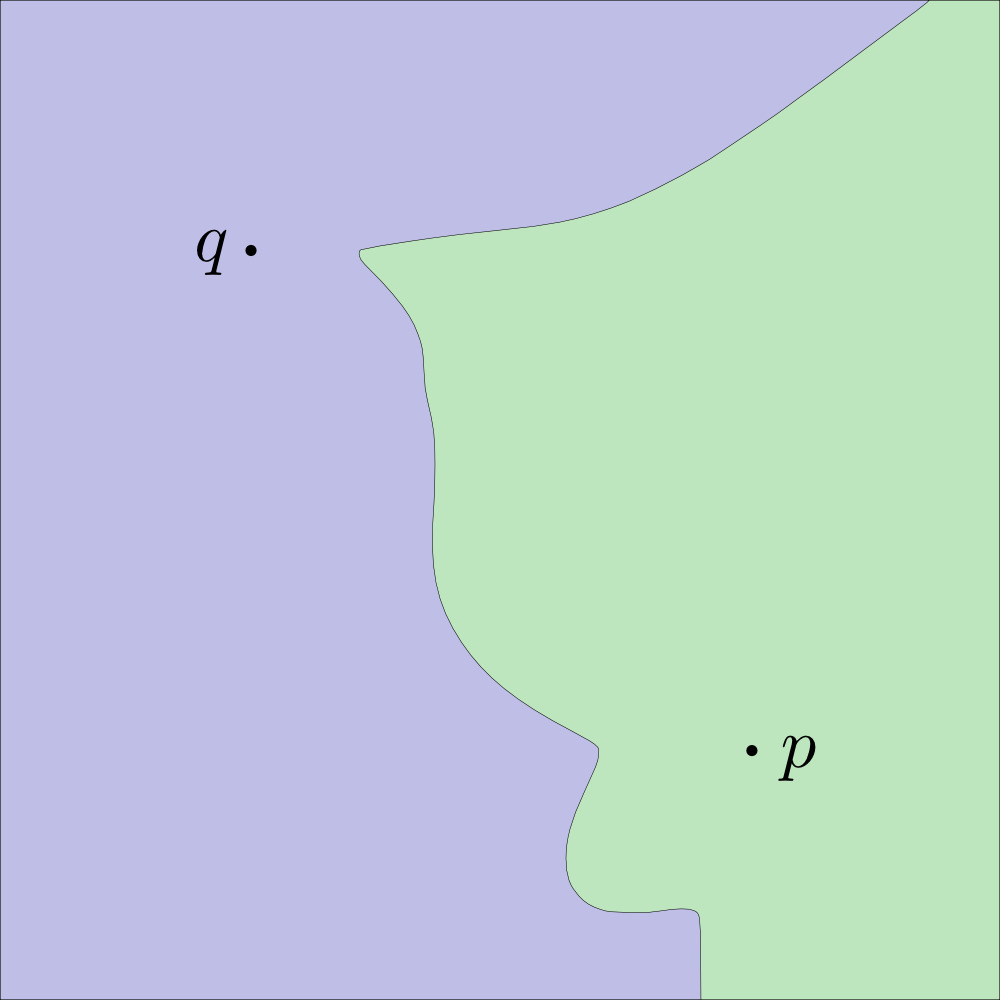 |
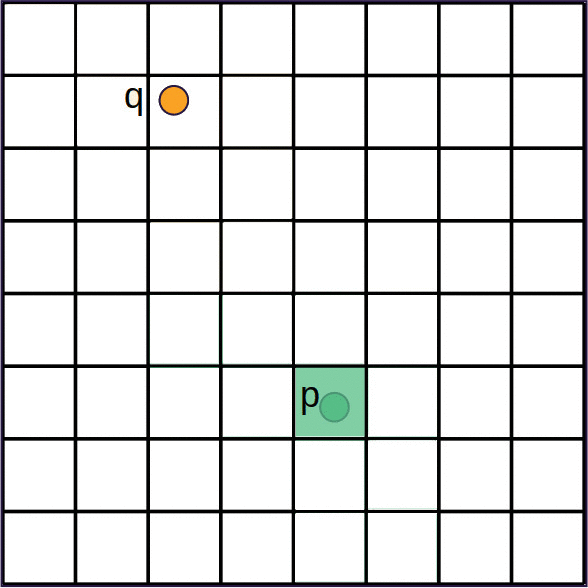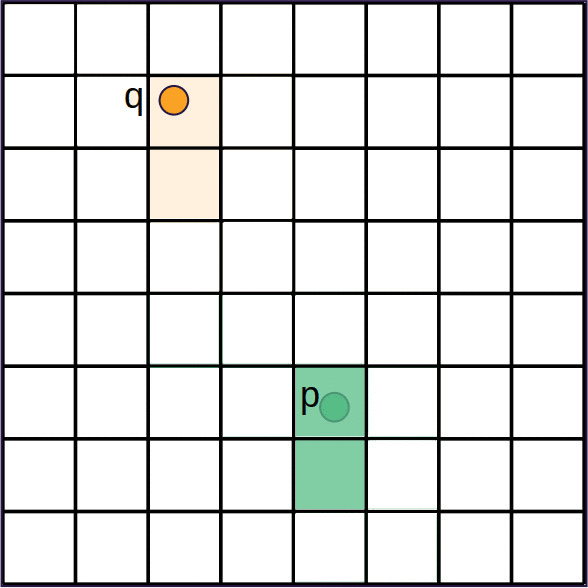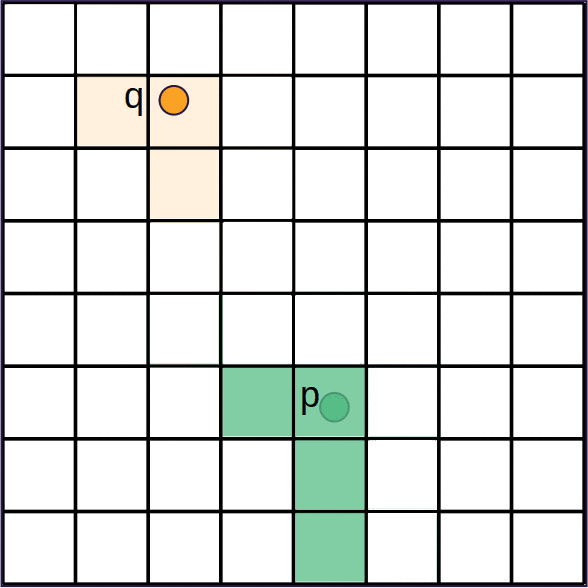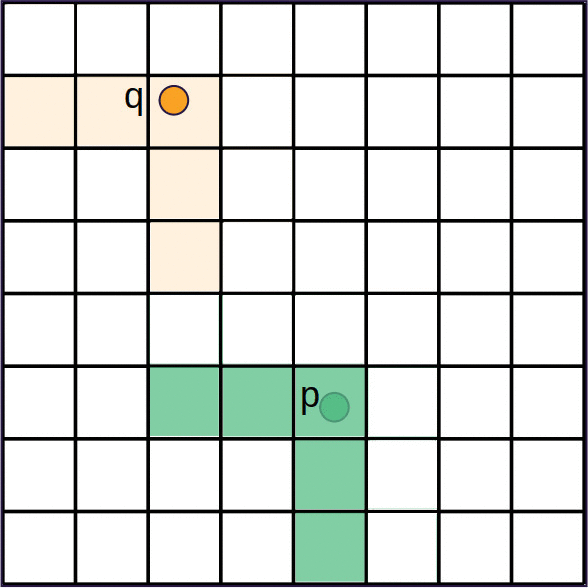
Discrete Growth Process Algorithm
priority queue of grid cells ordered by distance .
-
Insert in grid cells containing nuclei.
-
while is not empty do
- Pop grid cell from
- if is unlabeled then
- Label with originating nuclei
- Insert the -neighbourhood grid cells in
2D Point Lattices
| Diagonal | Triangular | Honeycomb |
|---|---|---|
 |
 |
 |
Symmetries
Point group symmetries lattice
Point group symmetries star-shaped set
subgroup shared symmetries
- The discrete growth process is (approximatively) invariant to any transformation of
- Example:

Three-fold rotation
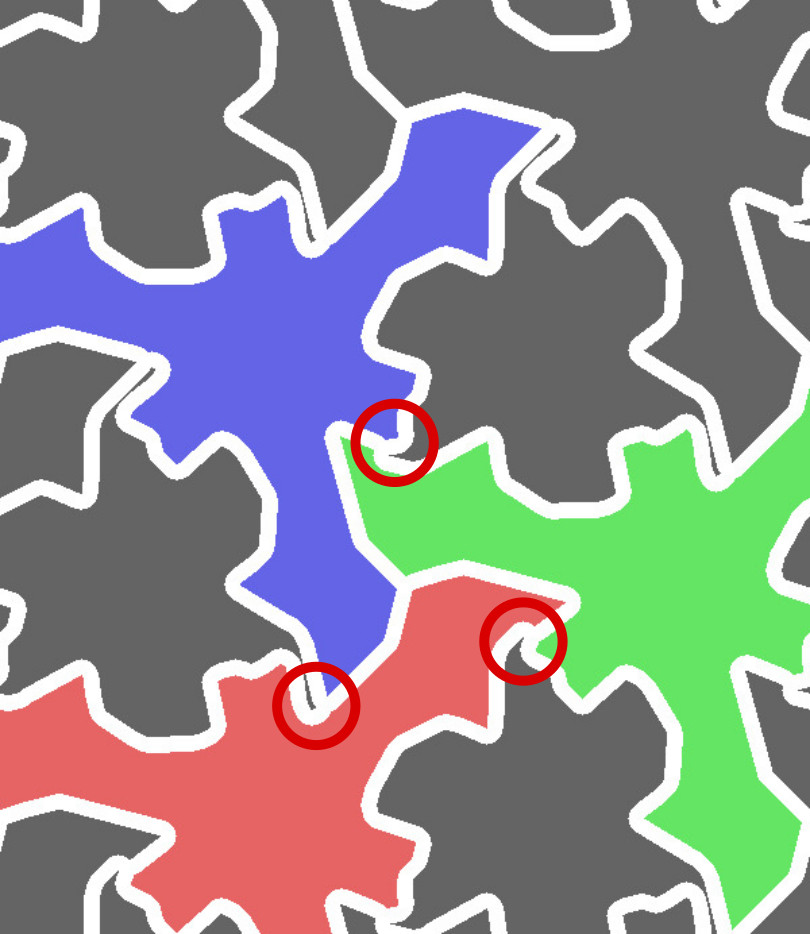
Growth Process Algorithm: Robustness
 |
 |
 |
 |
|---|---|---|---|
| Threefold symmetry? |
Growth Process Algorithm: Robustness
 |
 |
 |
 |
|---|---|---|---|
| Threefold symmetry |
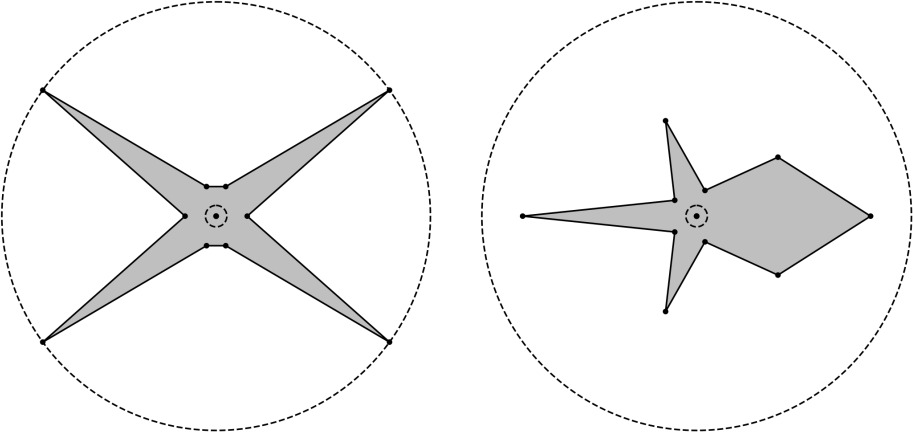
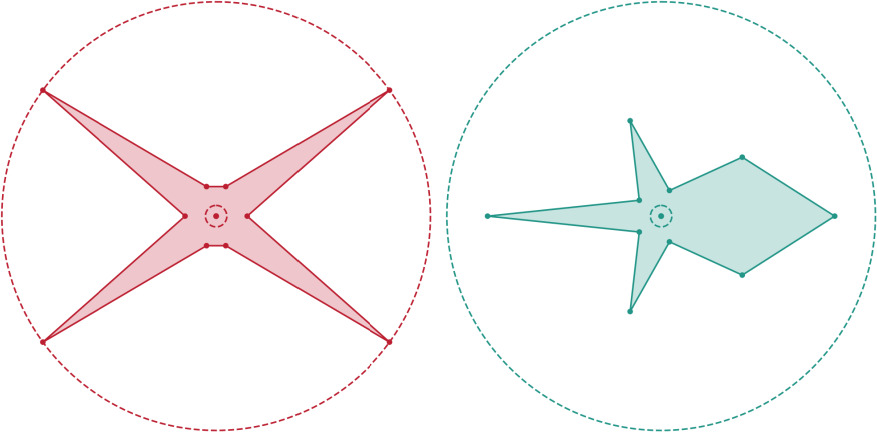
Grading
| Discrete | Continuous |
|---|---|
 |
 |
 |
 |
Isotropic Materials: Three-fold Rotation Symmetry
Orthotropic Materials: One-axis Reflectional Symmetry
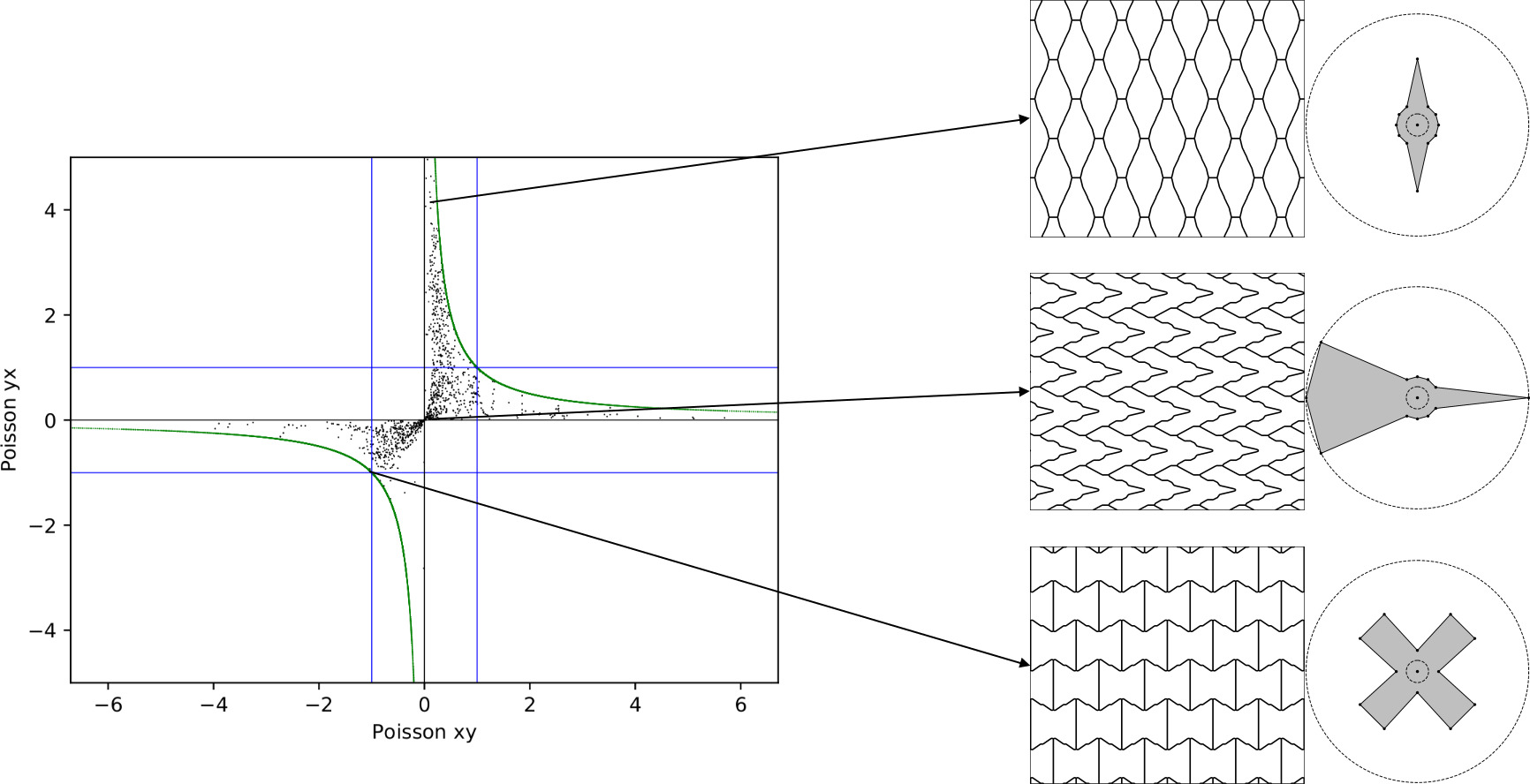
Printed Results
| Auxetic | Continuous grading | Discrete grading |
|---|---|---|
 |
 |
 |
 |
 |
 |
Contributions
| 2D Periodic | 2D Stochastic (auxetic) | 3D Periodic |
|---|---|---|
 |
 |
 |
Publication
Random Auxetic Porous Materials from Parametric Growth Processes
Jonàs Martínez
Computer-Aided Design 2021
Auxetic Materials
| Negative Poisson ratio | Applications |
|---|---|
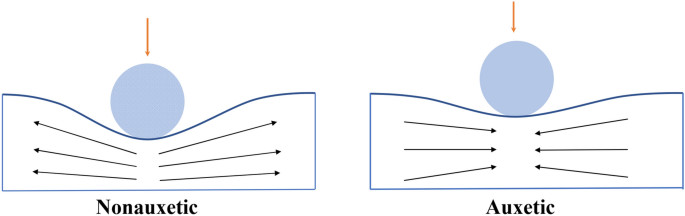 |
|
| Jian et al. 2018 | Excellent shock absorption, fracture toughness, or vibrational absorption |
Polymeric Auxetic Foams
| Uncompressed polyurethane foam | Tri-axially compressed |
|---|---|
 |
 |
| Mardling et al. 2020 |
2D Random Auxetic Networks
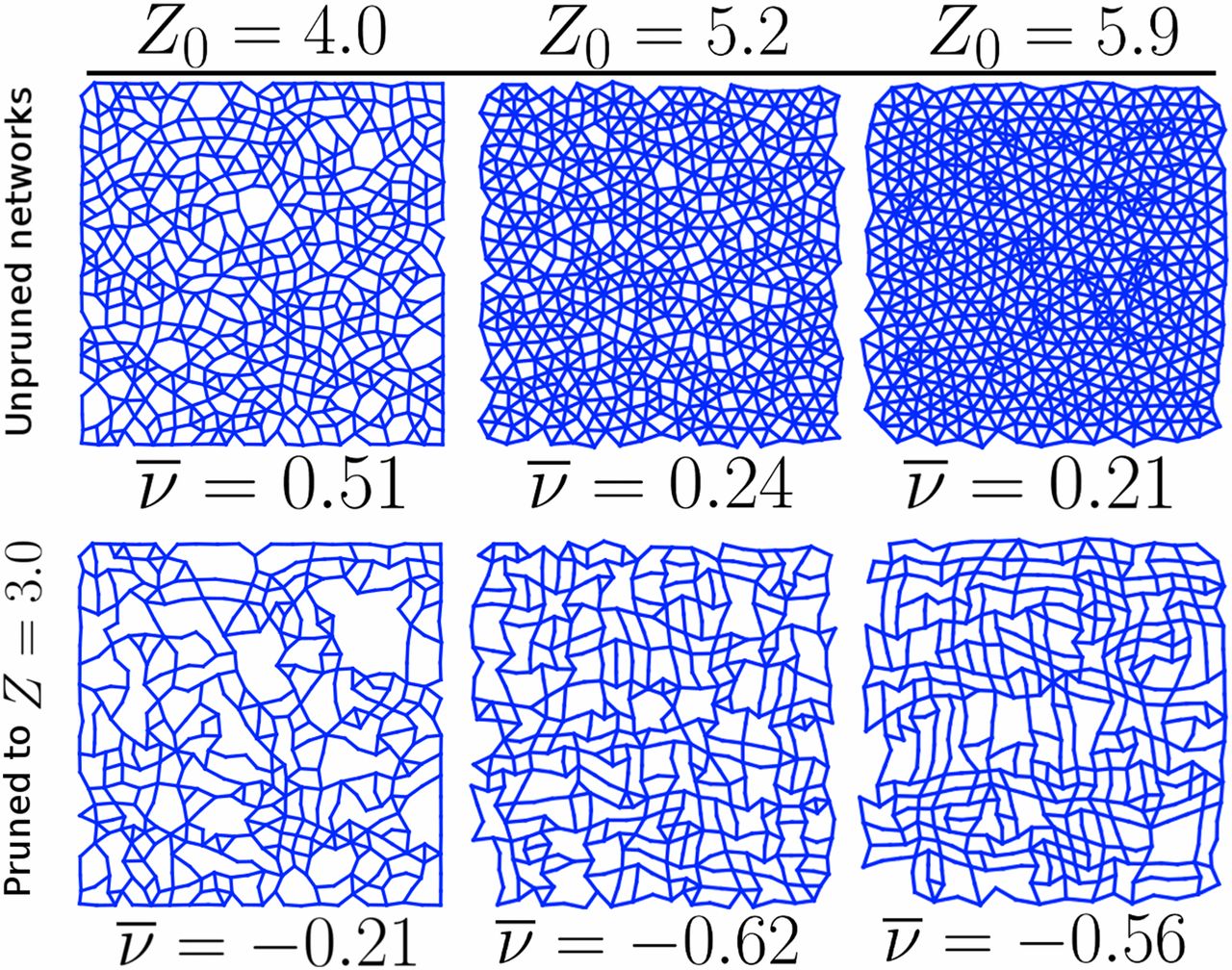 |
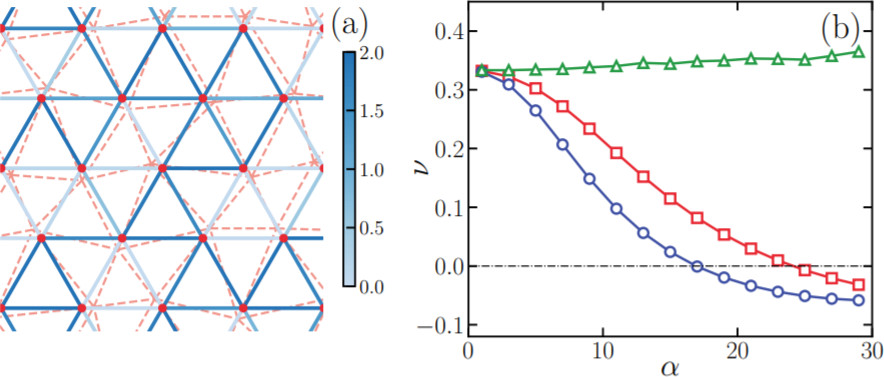 |
|---|---|
| Reid et al. 2018 | Liu et al. 2019 |
Random Materials
| Seamless geometry gradation | Isotropic elasticity | Symmetry-breaking resilient |
|---|---|---|
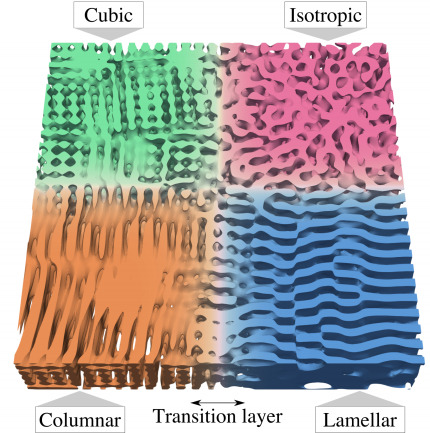 |
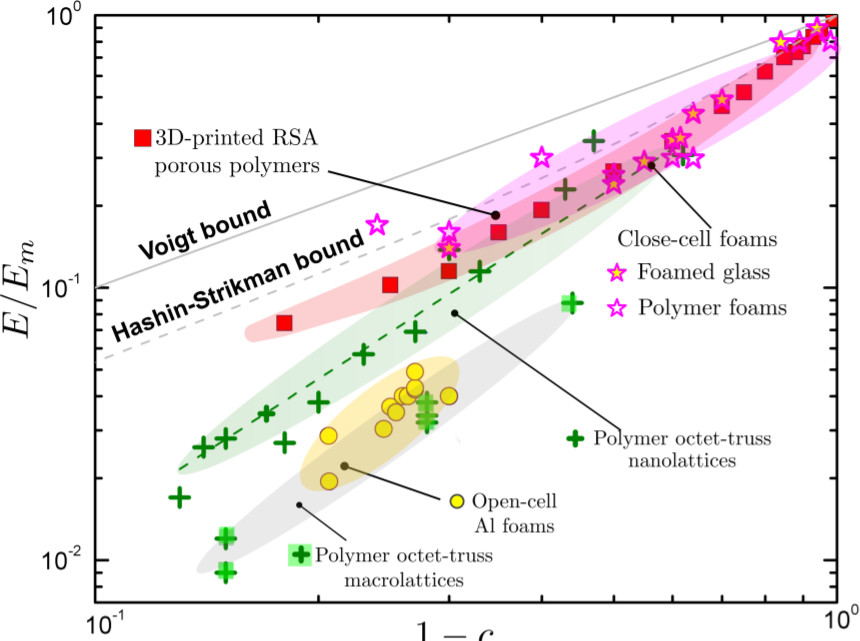 |
|
| Kumar et al. 2020 | Tarantino et al. 2019 | Portela et al. 2020 |
Our Approach
| Pre-processing | Porous Material |
|---|---|
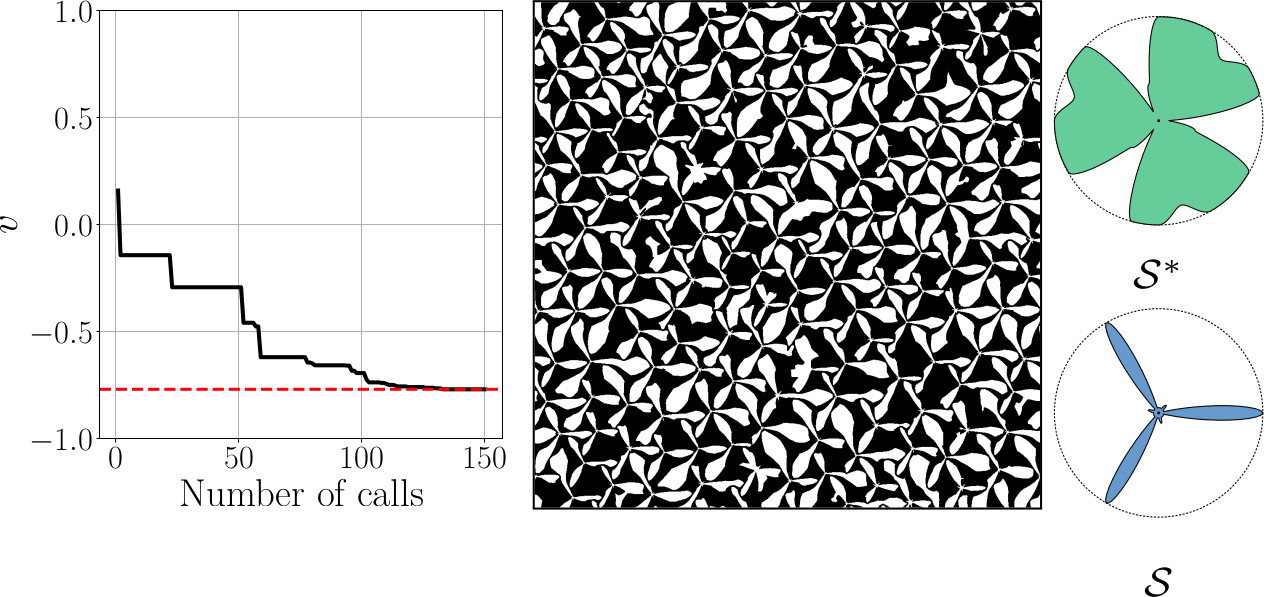 |
|
| Parametric optimization | Discrete Growth Process |
Parametric Growth Process
| Points | Distance | Thickness | Growth Process |
|---|---|---|---|
 |
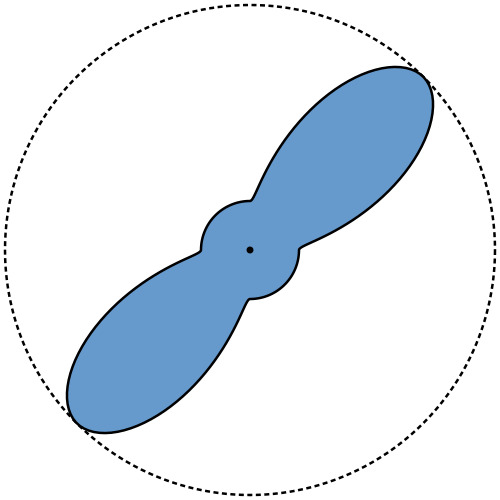 |
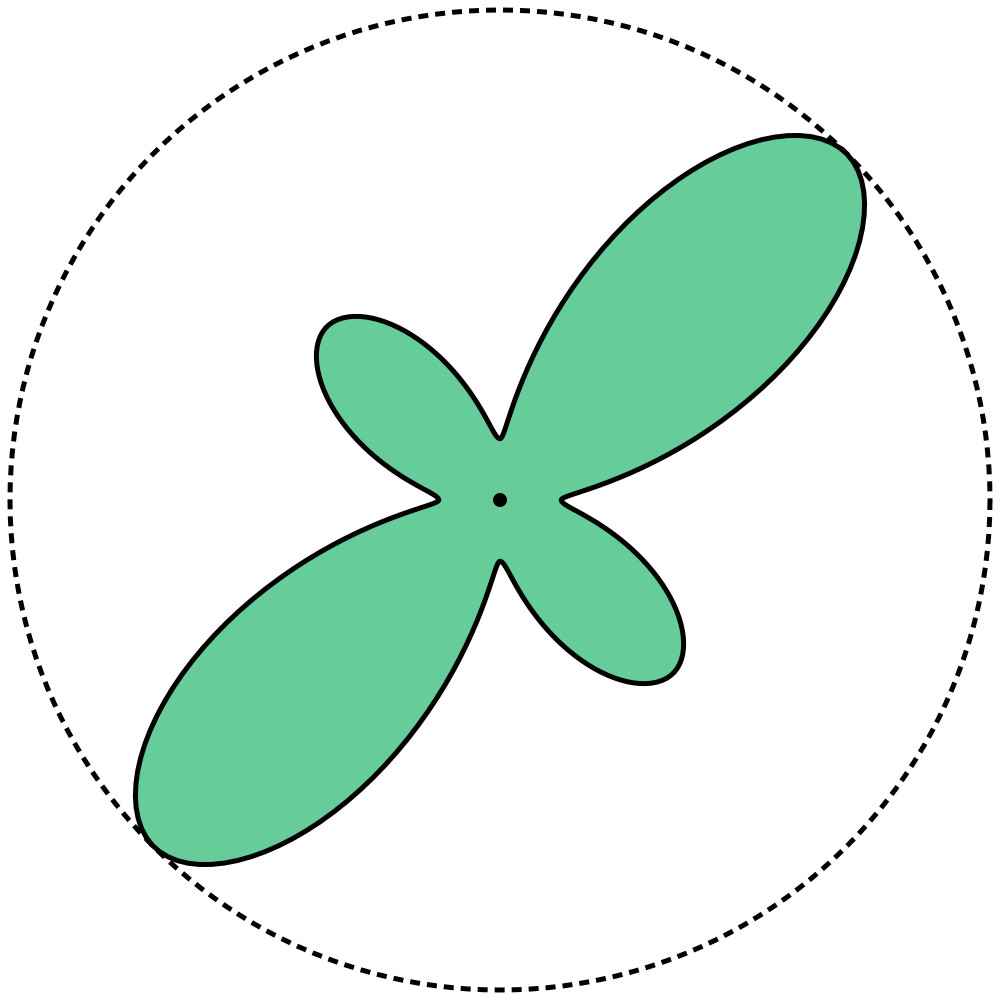 |
Cell Regularization
| Cell Growth | Non-regularized | Regularized | ||
|---|---|---|---|---|
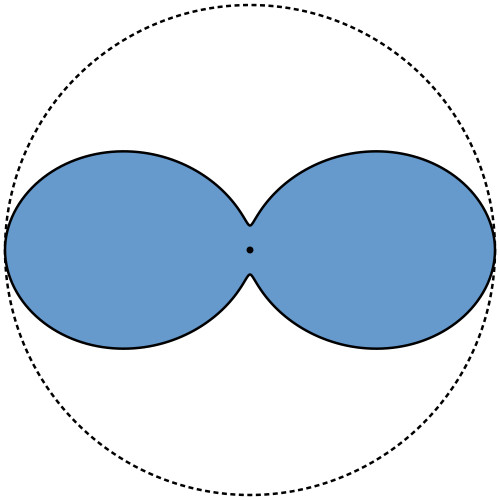 |
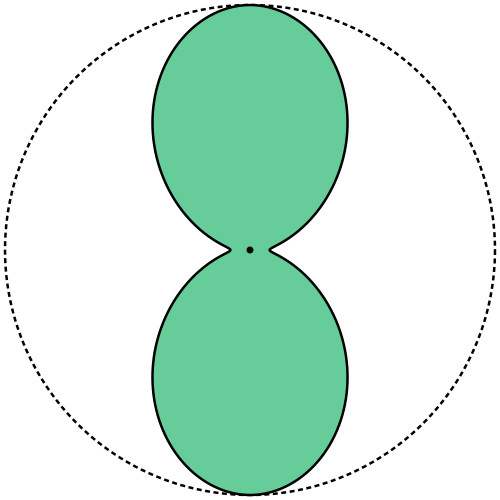 |
 |
 |
 |
- Numerical results show that cell regularization has little impact.
Stochastic Homogenization
- Hooke's Law:
Stress
Strain
Elasticity tensor
Isotropic Elasticity
- Closest isotropic elasticity tensor (closed-form):
- Deviation from isotropy :
Homogenized elasticity tensor
Frobenius norm
Three-fold Symmetry and Isotropy
Hypothesis
Let and be three-fold symmetric. The deviation from isotropy tends toward as the size of the growth process increases.
Three-fold Symmetry and Isotropy
Hypothesis
Let and be three-fold symmetric. The deviation from isotropy tends toward as the size of the growth process increases.
Intuition
- Rotation of angle around origin
- Let be a point (nucleus of a cell), for :
which hints that the discrete growth process is approximatively three-fold symmetric.
In 2D, three-fold symmetry leads to linear isotropic elasticity.
Three-fold Symmetry and Isotropy
Hypothesis
Let and be three-fold symmetric. The deviation from isotropy tends toward as the size of the growth process increases.
Numerical Results
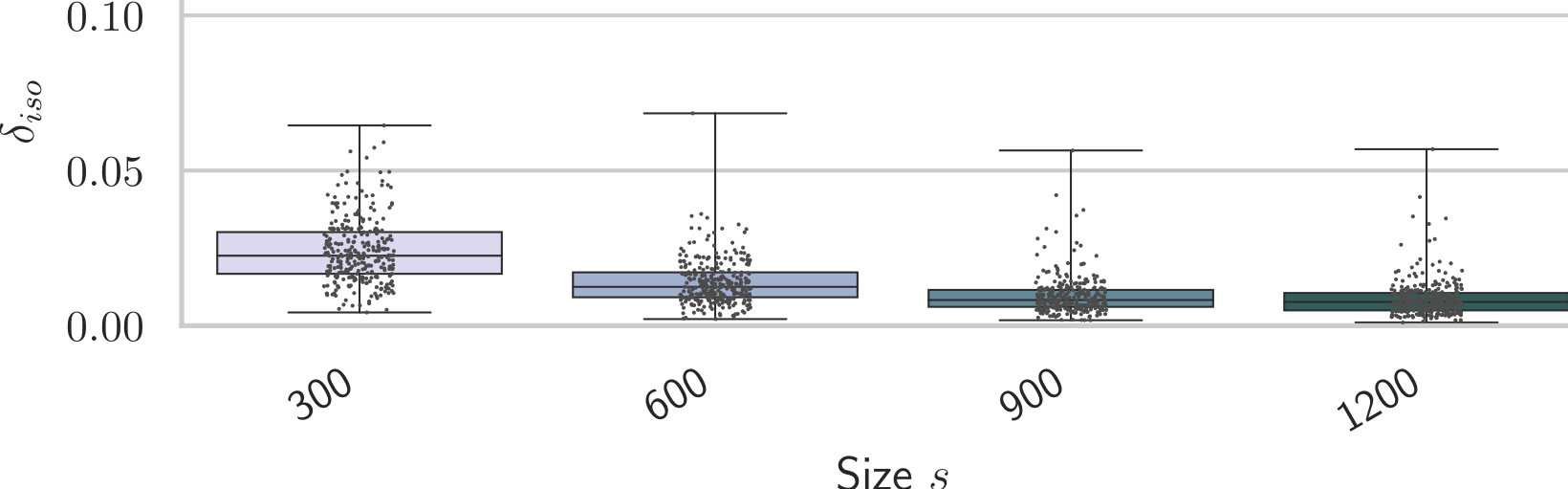
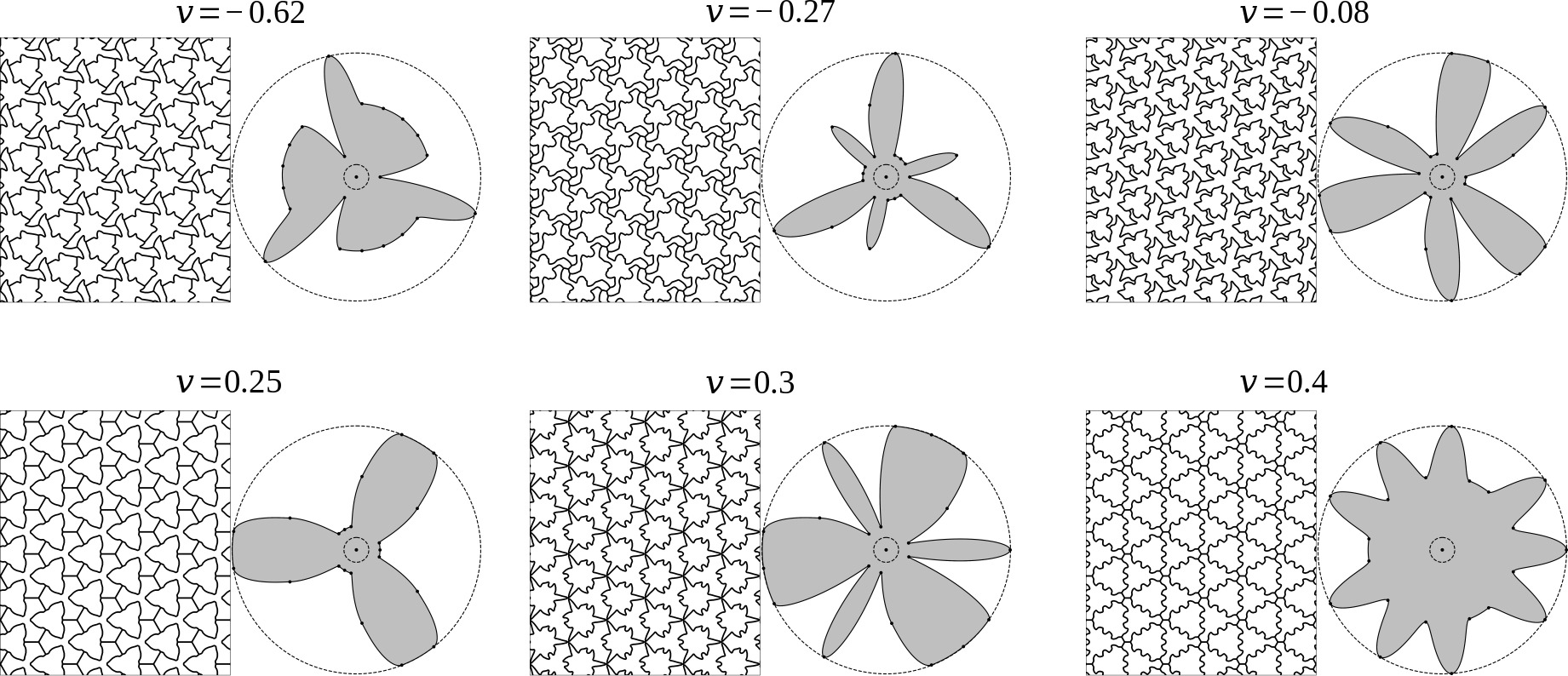
Isotropic Poisson's Ratio Minimization
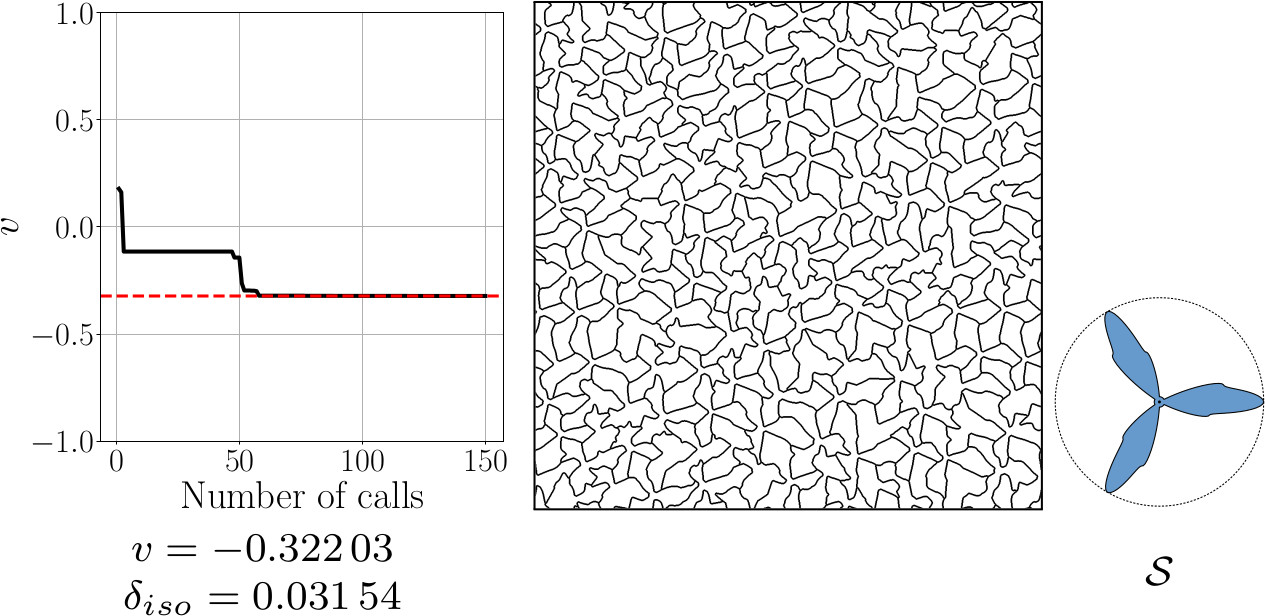
Isotropic Poisson's Ratio Minimization
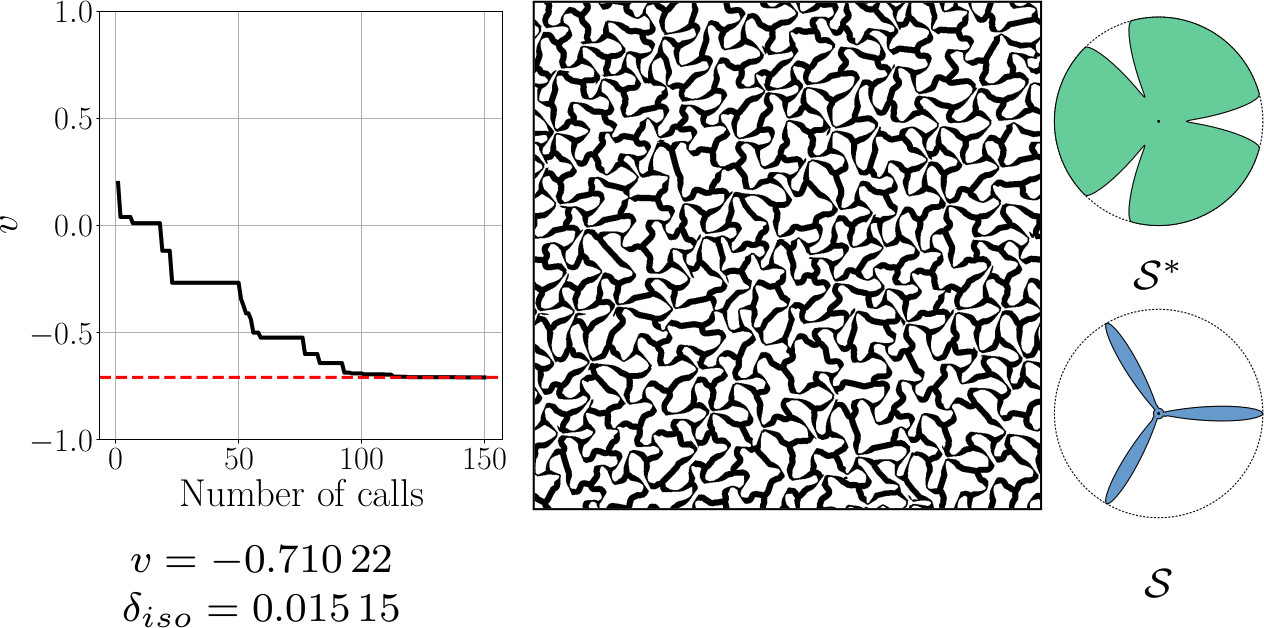
Isotropic Poisson's Ratio Minimization
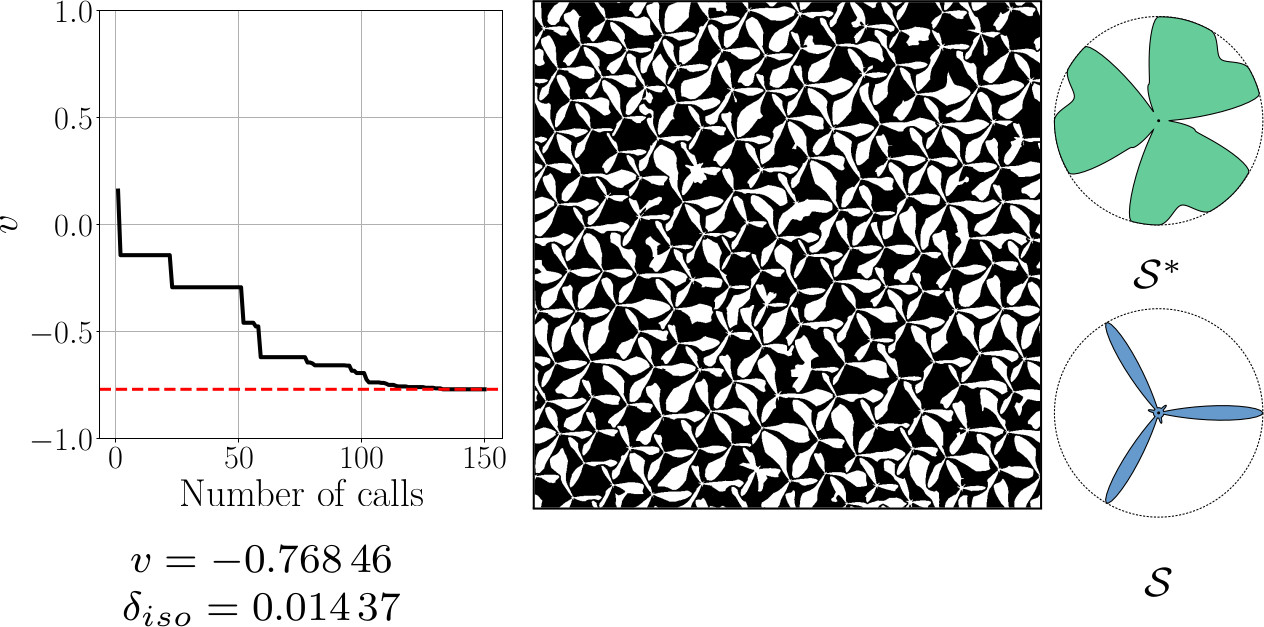
Experimental Results
- Laser-cut sheets made of Styrene-Butadiene Rubber (SBR).

Grading Results


Grading Results


Contributions: 3D Periodic
| 2D Periodic | 2D Stochastic (auxetic) | 3D Periodic |
|---|---|---|
 |
 |
 |
Publication
3D periodic Cellular Materials with Tailored Symmetry and Implicit Grading
Semyon Efremov, Jonàs Martínez, Sylvain Lefebvre
Symposium on Physical Modeling 2021
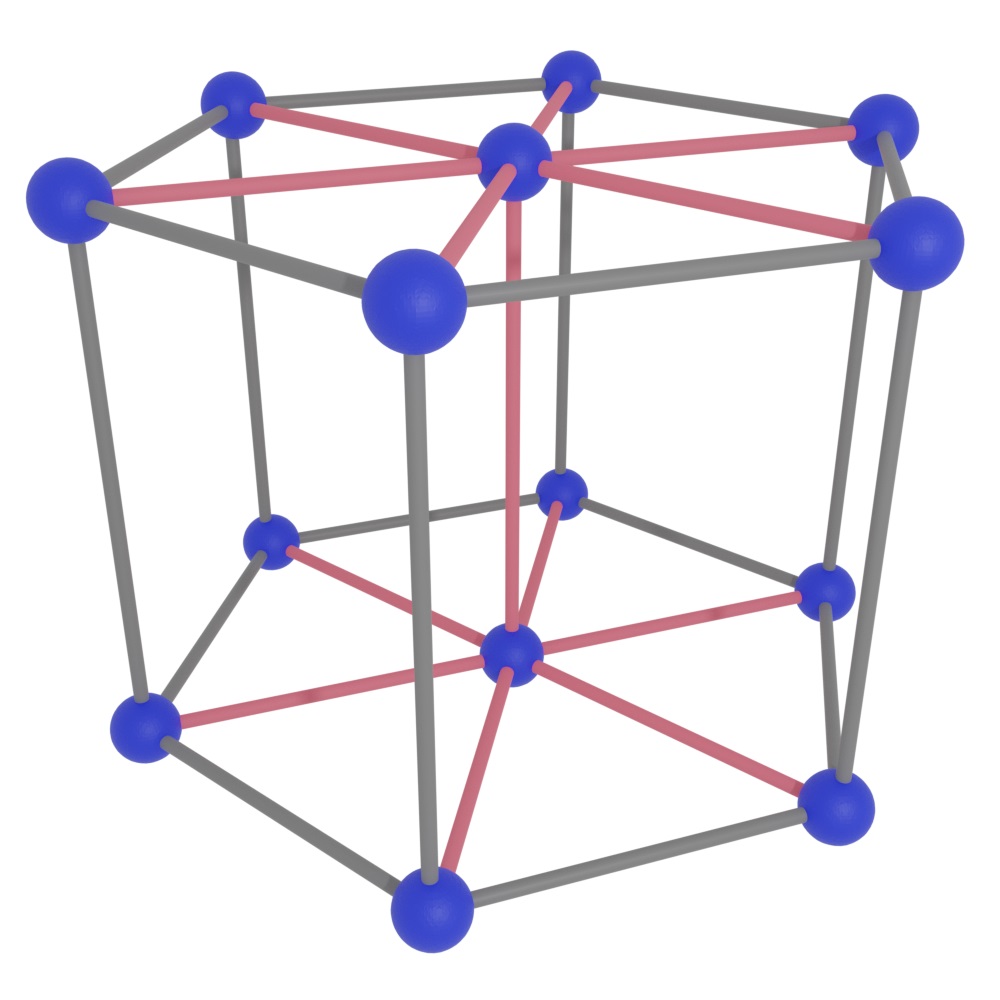
3D Parametric Growth Process
| 3D star-shaped set | Lattice | Growth Process |
|---|---|---|
 |
 |
  |
| Closed Cell 3x3 | Open Cell 3x3 | |
 |
 |
Crystallographic Symmetries
-
Geometric transformations (e.g., rotation, reflection) that leave the crystal unchanged
-
32 crystallographic point groups
-
Only (1,2,3,4,6)-fold rotational symmetries are possible
3D Lattice Parameterization
- Bravais lattices are periodic set of points defined as:
any integers.
primitive vectors
- Bravais lattices cover all crystal systems
3D Star-shaped set parameterization
| Spherical Harmonics | Spherical Polyhedra |
|---|---|
 |
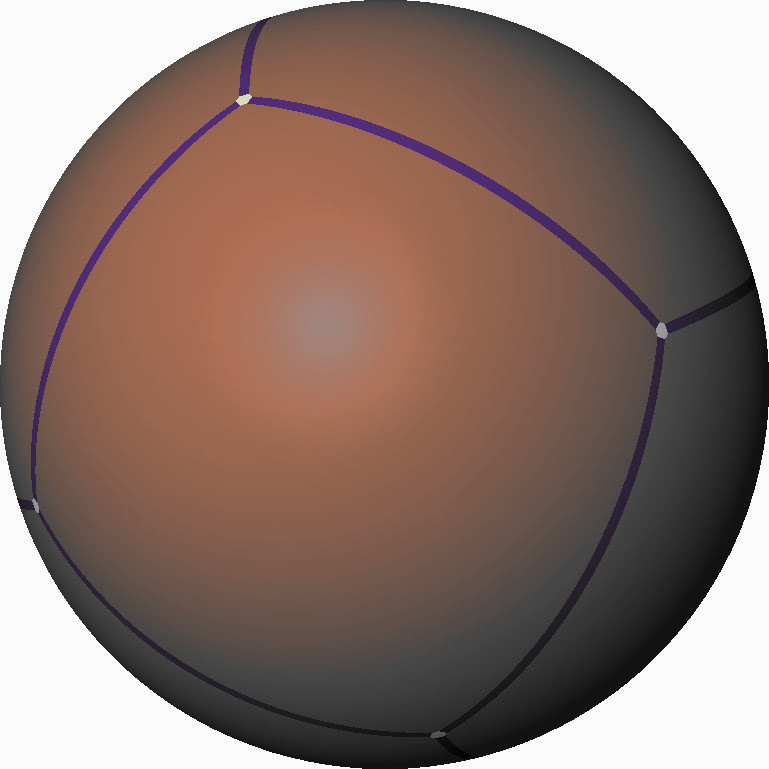  |
3D Symmetries
Point group symmetries lattice
Point group symmetries star-shaped set
subgroup shared symmetries
- The discrete growth process is (approximatively) invariant to any transformation of


Hexagonal symmetry
Geometry Gradation
  |
  |
  |
Numerical Homogenization
| Structure | Magnitude displacement | Von Mises stress |
|---|---|---|
 |
 |
 |
(1) Monchiet et al. A polarization-based FFT iterative scheme for computing the effective properties of elastic composites with arbitrary contrast, 2012
(2) Willot, Fourier-based schemes for computing the mechanical response of composites with accurate local fields, 2015
Geometric and Physical Symmetries
| Closed cell | Open cell |
|---|---|
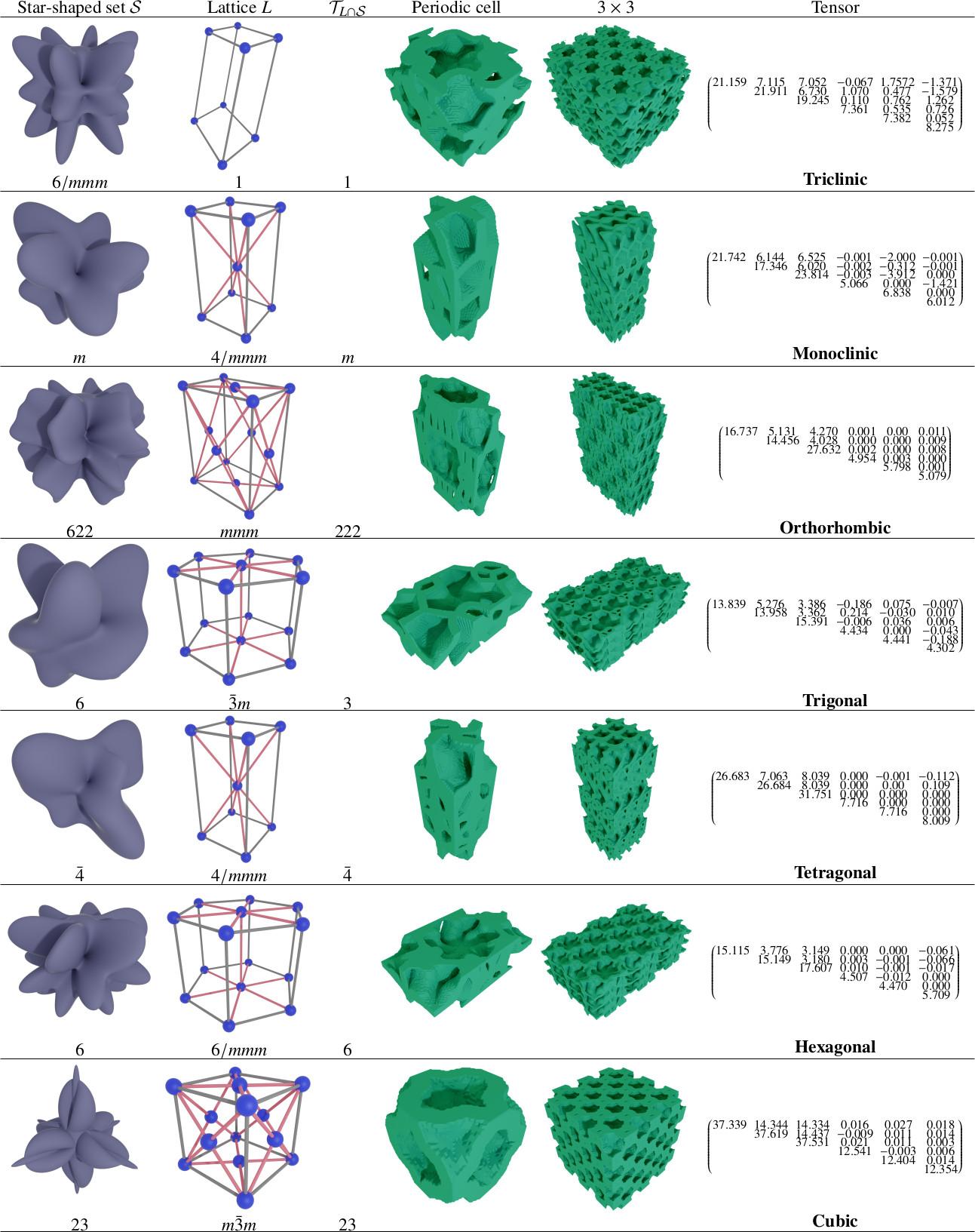 |
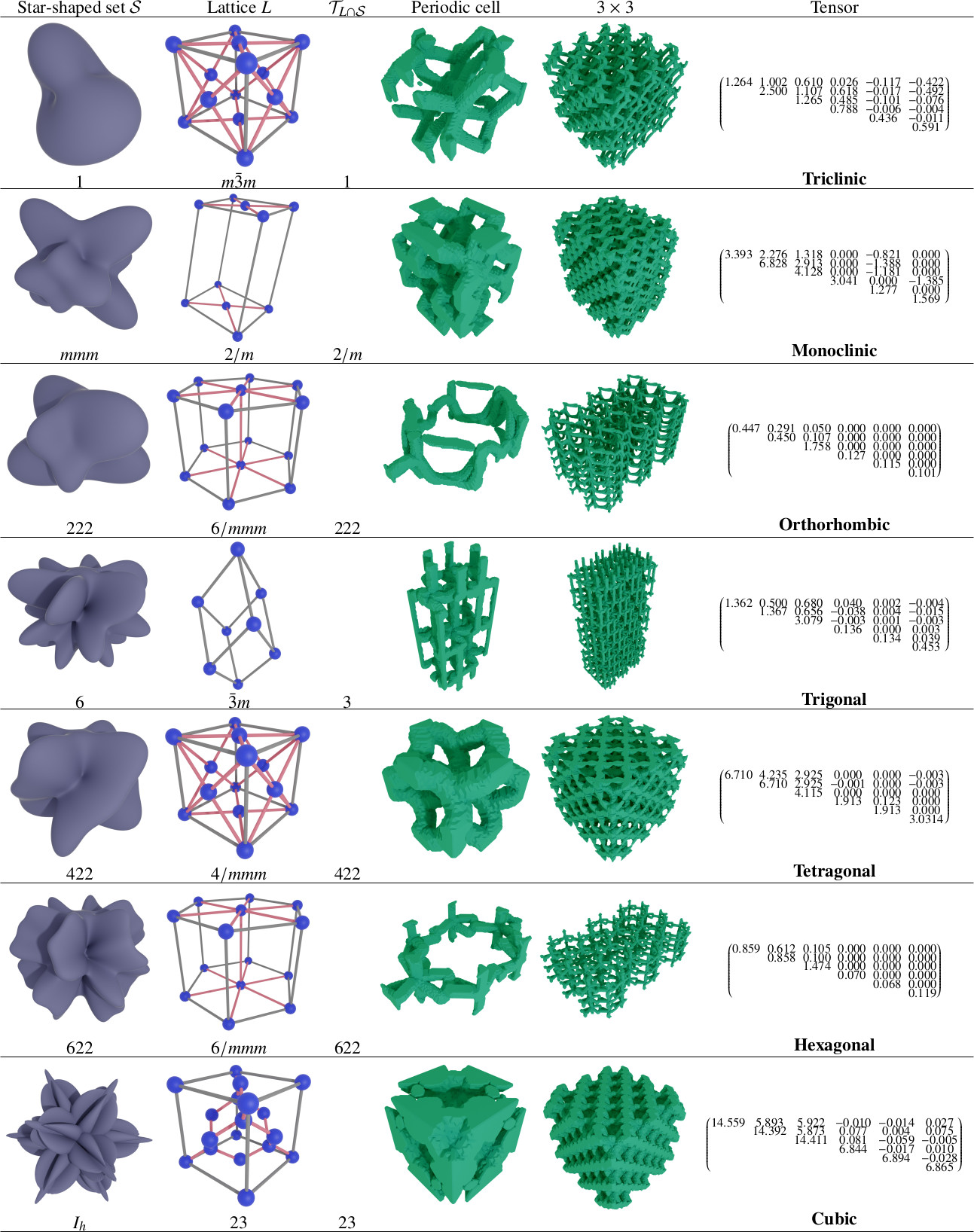 |
3D Printed Results
| Triclinic material | Monoclinic material |
|---|---|
 |
 |
3D Printed Results: Grading
 |
 |
|---|
3D Printed Results: Grading
 |
 |
|---|
Surface Frame Structure
| Rendered | 3D printed |
|---|---|
 |
 |
Limitations and Future Work
| Non-linear elasticity | Growth process | Beyond elasticity |
|---|---|---|
 |
 |
 |
Thank You
2D Periodic code
https://github.com/mfx-inria/starshaped2d